下書き Dürer & 測距儀2022d030 淡々と ddd 強行突破 答えから
光行差のことを 考えず
光線は ある一箇所の点位置へ
光速C 一定で 直進する設定で
俺が 見せたいものを
貴殿に 見てもらう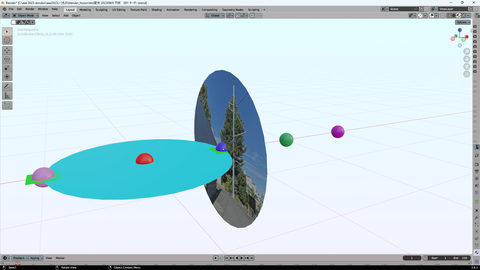
半径1の水色円板の 「円盤平面」宇宙船
1単位長さ 30万kmの イメージ
だから 円の中心に艦長として
点大きさで座る貴殿に
円板円周からの情報が 1秒後に届く
貴殿 赤玉 xyz= (0,0,0)
青玉 xyz=(0,1,0)
青玉を中心に 半径1の円で
写真を貼れる 丸形額縁を 作った
水色の Z=0 平面の
「円盤平面」宇宙船
床面を 非表示にした
Y=-1 薄ピンク玉
Y=0 赤玉 貴殿 位置
Y=+1 青玉 丸形額縁 中心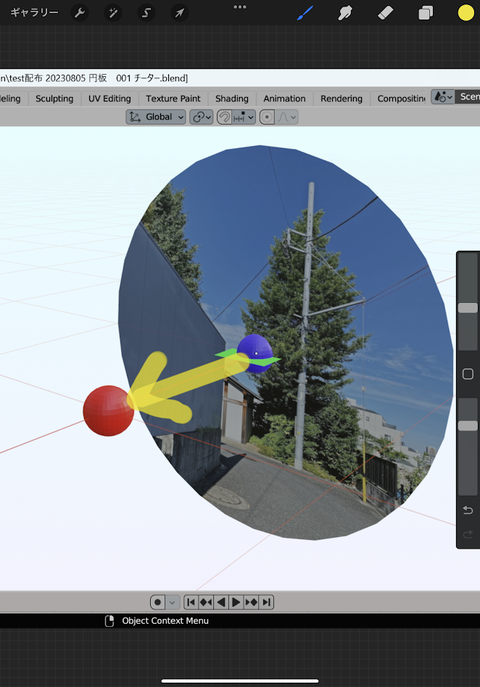
青玉が 発信した情報を
赤玉(貴殿)が 1秒後 受信する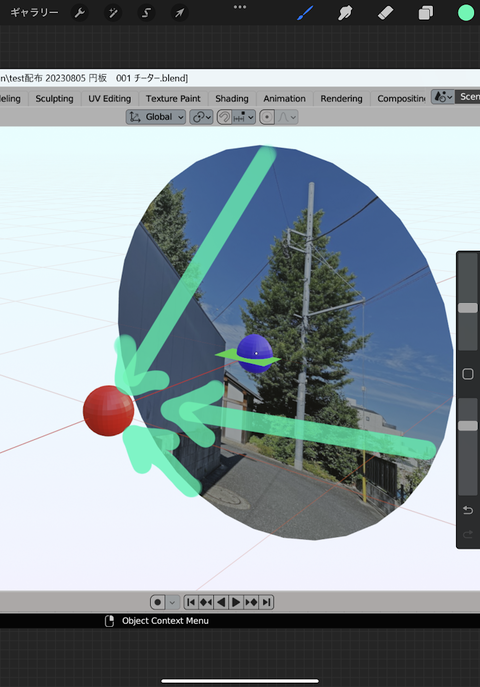
丸形額縁 円半径1
その円周を出発した情報が
赤玉(貴殿)に
√2秒後 到着する
絵図は 俯瞰図なので
Green 軌跡長さが
絵図上では バラバラに見えるが
1:1:√2 の
直角三角形 斜辺が Green 矢印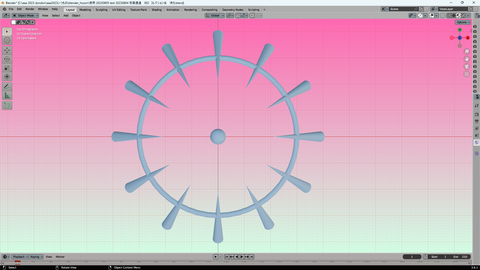
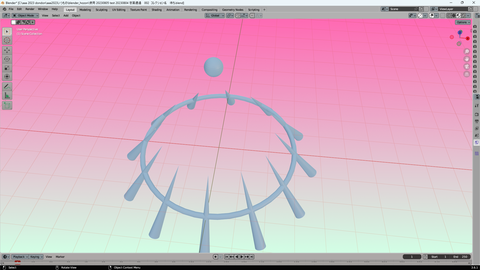
これは blender で 描いた半径3のトーラスだが
比率さえ一緒なら 形イメージ 同じなので
これを 使う
円周を通過した 円錐矢印の光線が
真ん中の 球体位置を目指す
円周が 半径1なら
1秒後に円周を通過した
描画されてる12の光線が 円中央に到達する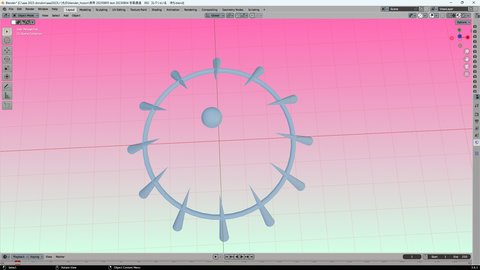
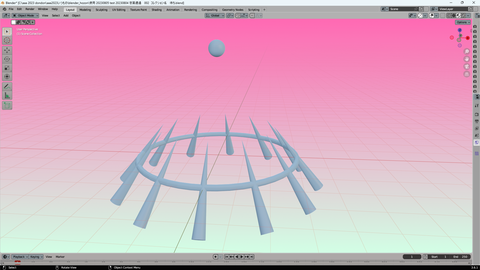
2次元平面の座標空間だと思っていたものが
3次元の座標空間だったのに
3枚の追加 画像を見て 気付いた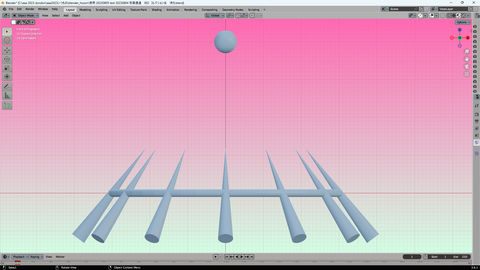
これは
横軸が X軸
縦軸が Z軸の
ZX平面 座標 
同じ位置で blender の 擬似的 俯瞰モード
遠近法の視座が この3次元空間内の
どこかに ある設定で描いた 平面絵図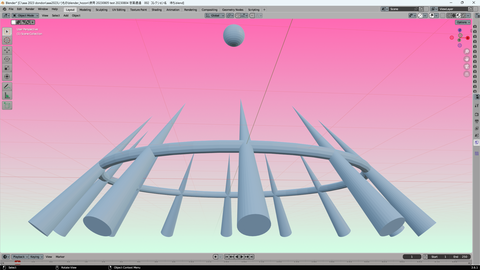
手前の円錐と
奥の円錐が
異なる 大きさで 描いてる
これは 物理とは 関係ない話
物理では どの円錐も
ここに 存在する12個の円錐大きさは 同じ
立ち位置 視座で 大きさイメージが
異なるように見えたのは
見てくれ
見かけ
で あって 物理には 直接 関係ない話
存在は
視座(立ち位置)によって
変化しない
存在は
視座(立ち位置)によって
「見かけ」が 変化する
「見かけ」には
3次元空間内の 点大きさ カメラアイにとってのと
「見かけ」には
視座なしの
座標空間 設定で 生じるものがある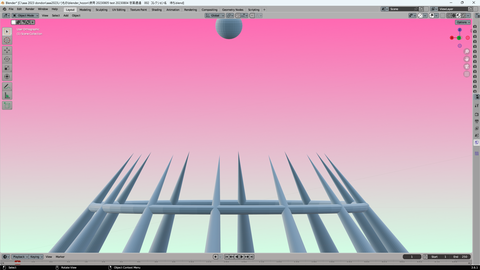
座標空間設定で 生じるものとは
半径1(又は3)のトーラス 1つ
1つの小さめ 球体
12個の 棒状 円錐
からなる 被写体群 「ひとまとまり」が
フレーム枠内に 収まってないとか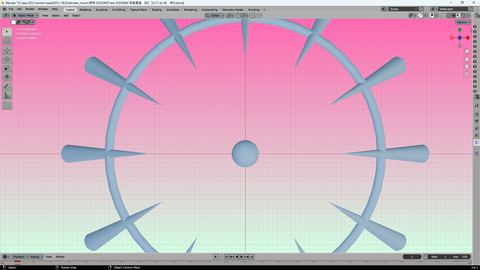
+Z軸 真上から 描画指定すると
円錐底面が 見えていない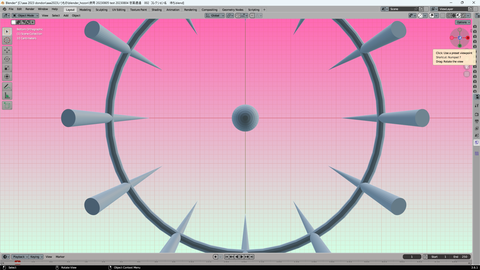
ーZ軸から 描画すると
円錐底面が 見えてる
これらは オブジェクト存在が 変化したのではなく
描画していの断面が 異なってるからである
それと 同様なことが
列車横姿の輪郭線だけに注目し
相対速度0での 列車慣性系 断面描写
聡太速度Vでの 列車慣性系 断面描写で
列車搭載 光時計内 光線先端 軌跡
t=0から
t=1に
縦線 に見えるか
斜線に 見えるかで
光線軌跡の 長さが
物理的に 変わってしまったと思い込んだのが
19世紀生まれの方々で
20世紀 生まれでも
物理業界では
ただの 勘違いを 修正できなかったのが
いままで
その説明を 強行突破で 始める
「円盤 宇宙船」 艦長席(0位置)は
半径1の 中心
貴殿は 速度不明ながら
Green 位置 -1から
2秒で
ちょい薄青 +1位置へ
動いた
ピンク矢印 方向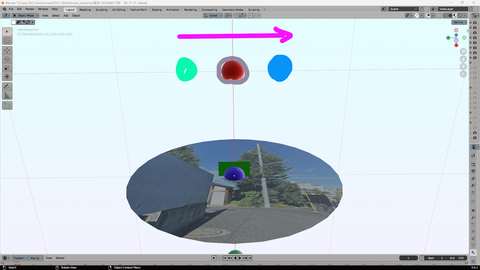
丸形額縁 写真貼った平面に
平行に 貴殿が 動いた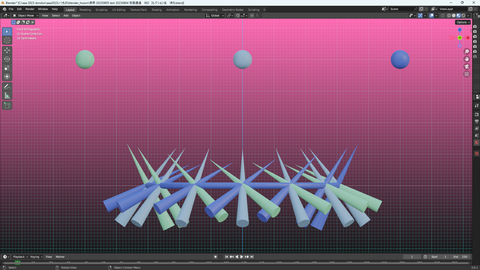
作製 絵図によって
x軸
y軸
z軸の 採用が バラバラなんで
絵図内の 上下左右で 表現させてもらう
丸形額縁 円周が不動
丸形額縁を 線路レール慣性系に 見立てる
「円盤平面」宇宙船内を移動する貴殿
点大きさが 列車慣性系
面倒なんで ここでの横軸を X軸と呼称
絵図内の blender の軸線方向を 無視する
高さ方向 Z軸
貴殿の移動は Z=1平面内
丸形額縁存在は Z=0 平面内
貴殿は t=-1に
Z=+1の
X=-1に 存在した
丸形額縁 存在から 高さ1の平面を
貴殿は 移動中
時刻 不明ながら
t=-1の 貴殿存在に
情報を伝えようと
丸形額縁 円周各点から光線が出発した
円周各点から
t=-1の
Z=1
X=-1
さらに Y=0
に 同時到着するように
バラバラの時刻
バラバラの方向へ
光線が 出発した
丸形額縁は xyz座標空間では
x^2+y^2+Z^2=1 の
円周であるが
ZX平面では 長さ2の線分姿に なってる
だから zx平面だけで
光線発射位置 複数と
光線の
到着位置と
到着時間を 計算するのは ミスである
球体は 3次元空間内の
どこから 見ても
同じであると 思われるが
点大きさのカメラアイを
3次元空間内に 設置
球体は 大きさ違いあれど
円に見える
同様に
xy平面に 球体を投影しても
yz平面に 球体を投影しても
zx平面に 球体を投影しても
円イメージになる
球体からの投影平面 遠さ位置を考慮すれば
カメラアイの視野広さのような
投影平面 断面に 有限大きさの 窓面を
設定すると
円イメージの大きさが
断面 窓枠に対して
大きくなったり
小さくなったりする
座標空間であっても
点大きさのカメラアイのように
被写体の 「見かけ」イメージが
発生している
カメラアイに
被写体 表面からの光線が届く
近接作用による 情報遅延は 物理だが
カメラアイの立ち位置によて
被写体の見かけが 異なるので
逆算して 被写体「存在」 そのものを
描写 しようとする
それと 同様に ここでの
ZX平面に描いた
円周各点から
t=-1
x=-1
Z=+1
そして Y=0に
光線が 同着するように
発射時刻と
発射方向を 求めるのを
ZX平面だけで やれば 計算ミスとなる
つまり 言いたいことは
光線発射 位置形態は 2次元の円周各点
光線到着 位置形態は 0次元の点大きさ
この非対称では 計算ミスが生じてるのに
気付かない 気付きにくいので
光線発射 形態も
光線到着 形態も 同じ 次元の大きさで
計算する
数学世界の
1対1 対応
1対多 対応
多対多 対応 で 整理して
列車慣性系では
列車内の 光時計が
縦方向 長さ 1なのに
線路慣性系からは√((c^2)+V^2)
縦方向と横方向の
合成長さに 見えるって事自体が
恣意的な 空間断面の使用
座標空間での 断面図 投影面での
使用に 手続きが 物理としてなく
それを元に 計算だけして
ローレンツ短縮だの
時空連続体 仮説 などで
誤魔化しに気付かなかったのが
いままで
それを 具体的に 調査する